◎ オームの法則 (Ohm's Law)
ドイツ人のオーム(Geoge Simon Ohm 1787〜1854)によって発見された法則。
定義: 導体(抵抗体)を流れる電流はその導体の両端にかかる
電圧(両端の電位差)に比例する。 |
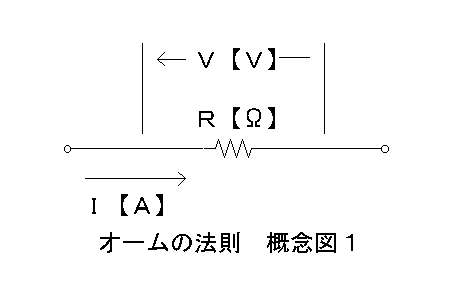
流れる電流をI【A】、導体の持つ抵抗をR【Ω】、電位差をV【V】とした時、
一般に以下の関係が成り立つ。
この等式を意味的に解釈すれば、以下のことが言える。
- 導体を流れる電流Iは電圧Vに比例し、導体抵抗Rに反比例する。
- 導体両端の電位差Vは導体抵抗R及び、電流Iに比例する。
- 導体が持つ抵抗Rは電位差Vに比例し、電流Iに反比例する。
また、これらの事は定義式の上でも明らかである。
公式: V=IR を変形すれば、オームの法則は3通りの等式で表せる。
- V=IR
- R=V/I
- I=V/R
今、ここに以下の図のような回路を組み立てて実験を行えば、
オームの法則が成り立つことを確認できる。
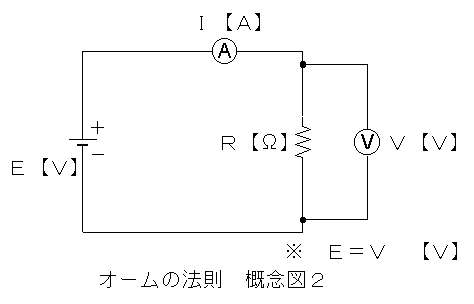
接続する直流電源の電圧値を徐々に上げていき、その時の電流計Aの
指示値をデータとして採ると、電圧に対して電流が比例して増加していく。
例として、100【Ω】の抵抗をつないだ場合のデータ表の一例を以下に示す。
オームの法則の確認実験(サンプル)
| 電圧V 【V】 |
電流I 【mA】 |
| 1 |
11 |
| 3 |
29 |
| 5 |
50 |
| 10 |
98 |
| 15 |
152 |
抵抗R=100【Ω】一定
このデータ表をグラフ用紙上にプロットし、電流―電圧グラフを作ると、以下のようになる。
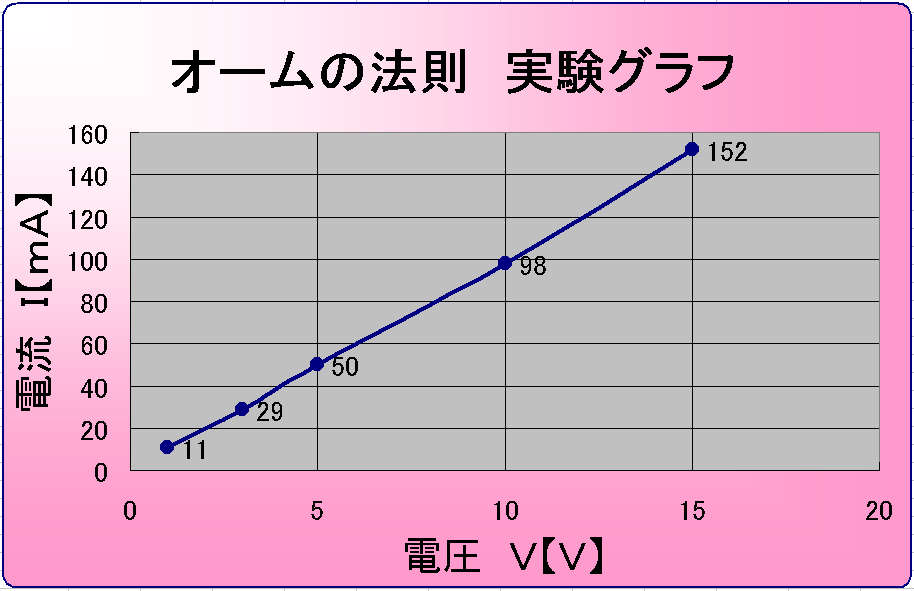
このグラフを見ると、誤差等の影響によって多少グラフが歪んでいるものの、
V―I間に比例関係があることが認められることと思う。
◎ 抵抗体の形状による抵抗値の変化
導体が持つ電気抵抗は、その大きさや形状に依存して変化する。
定義: 一様な材質を持つ導体について、抵抗は導体の長さに比例し、
断面積の大きさに反比例する。 |
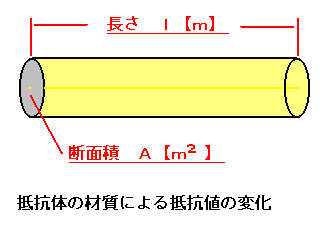
一般に、導体の抵抗値をR【Ω】、長さをl【m】、断面積をA【m2】とすれば、
Rは以下の形で表せる。
この時、ρは「ロー」と読むギリシャ文字で、その導体の材質が持つ抵抗率ρ【Ω・m】という。
抵抗率ρは材質によって異なる値を示すが、以下に一般的な材質の抵抗率を示す。
※ 常温 20【℃】時
| 金属 |
抵抗率ρ【nΩ・m】 |
| 金 |
24 |
| 銀 |
16.2 |
| 軟銅 |
17.2 |
| 純鉄 |
98 |
| アルミニウム |
27.5 |
◎ 温度による抵抗値の変化
導体の抵抗値は、それが置かれている場所の温度によっても変化する。
この変化を考えるためには、温度係数という概念を用いる。
| 定義: 温度が1℃変化した時に抵抗が変化する割合を温度係数という。 |
ある材質が温度t【℃】においてRt【Ω】の抵抗値を持ち、温度係数がαt【1/℃】
であった。この材質がT【℃】になった場合の抵抗値RTは以下の式で表せる。
この関係式は非常に覚えにくい。なので、単純に丸暗記せず、その式が
表すことを概念的に覚えると良い。
変化前後の温度差T−tの温度係数αt倍に1を足し、変化前の抵抗値Rtを
かければ変化後の抵抗RTが求められる。



